Uma placa plana infinita, de espessura , possui uma densidade volumétrica de carga uniforme (Figura 2.27). Encontre o campo elétrico, como função de , onde no centro. Faça um gráfico de versus , chamando de positivo quando apontar na direção e de negativo quando apontar na direção .
Passo 1
Falaaa, tudo belezaa?? Para acharmos o campo elétrico com a lei de Gauss usamos a fórmula abaixo:
Quer dizer que a integral do campo elétrico em uma superfície fechada é igual a carga envolvida dividida por uma constante. O que precisamos agora é definir a superfície e a carga envolvida. Bora lá!!!
Passo 2
A superfície fechada deste exercício será um cilindro que aumentará na direção de , então, vamos considerar a superfície fechada como .
O enunciado nos diz que a placa possui uma densidade volumétrica, então, .
Onde, . Substituindo os valores.
Porém, quando , quer dizer que o campo está para fora da placa, e a carga envolvida agora é: . Sendo assim, o campo resulta em:
E o gráfico de em função de pode ser descrito como:
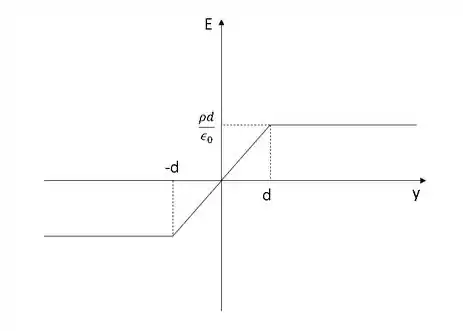
Resposta
Para :
Para :