Pode-se pensar em um dipolo elétrico em rotação como a superposição de dois dipolos oscilantes, um ao longo do eixo e o outro ao longo do eixo , estando o segundo fora da fase por :
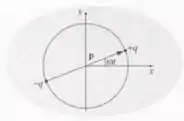
Usando o princípio da superposição, encontre os campos de um dipolo em rotação. Encontre também o vetor de poynting e a intensidade de radiação.
Passo 1
Fala aiii meus lindos tudo blz? espero que sim
Então se liga só nessa questão do livro David J. Griffiths de Eletrodinâmica pode-se pensar em um dipolo elétrico em rotação como a superposição de dois dipolos oscilantes, um ao longo do eixo e o outro ao longo do eixo , estando o segundo fora da fase por :
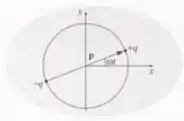
Usando o princípio da superposição, encontre os campos de um dipolo em rotação. Encontre também o vetor de poynting e a intensidade de radiação.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Sabendo que,
Temos,
E por fim na letra (d) para mostrar que a soma das forças é igual a menos a taxa de variação temos,
Ficando,
Logo,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta