Segundo a lei de Snell, quando a luz passa de um meio oticamente denso para outro menos denso o vetor de propagação desvia-se afastando-se de normal. Em particular, se a luz incide no ângulo crítico
Então , e raio transmitido simplesmente passa rasante à superfície. Se exercer , não haverá raio retratado de forma alguma, somente um raio refletindo (esse é o fenômeno de reflexão interna total, no qual os tubos de luz e as fibras óticas se baseiam). Mas os campos não são nulos no meio ; o que obtemos é a chamada onda evanescente, que é rapidamente atenuada e não transporta energia para o meio .
Uma maneira rápida de construir a onda evanescente é simplesmente citar os resultados de ,
A única alteração é que,
Agora é maior que 1 e
a) mostre que,
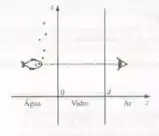
Esta é uma onda propagando-se na direção x.
b) observando que é agora imaginário para calcular o coeficiente de reflexão para polarização paralela ao plano incidente.
c) faça o mesmo para a polarização perpendicular ao plano de incidência.
d) em caso de polarização perpendicular ao plano de incidência, mostre que os campos evanescentes reais são
e) verifique se os campos em (d) satisfazem todas equações de Maxwell.
f) para os campos em (d), construa o vetor de e mostre que, na média, não há transmissão de energia na direção
Passo 1
Fala aiii meus lindos tudo blz? espero que sim
Então se liga só nessa questão do livro David J. Griffiths de Eletrodinâmica segundo a lei de Snell, quando a luz passa de um meio oticamente denso para outro menos denso o vetor de propagação desvia-se afastando-se de normal. Em particular, se a luz incide no ângulo crítico
Então , e raio transmitido simplesmente passa rasante à superfície. Se exercer , não haverá raio retratado de forma alguma, somente um raio refletindo (esse é o fenômeno de reflexão interna total, no qual os tubos de luz e as fibras óticas se baseiam). Mas os campos não são nulos no meio ; o que obtemos é a chamada onda evanescente, que é rapidamente atenuada e não transporta energia para o meio .
Uma maneira rápida de construir a onda evanescente é simplesmente citar os resultados de ,
A única alteração é que,
Agora é maior que 1 e
a) mostre que,
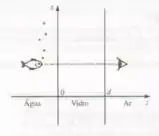
Esta é uma onda propagando-se na direção x.
b) observando que é agora imaginário para calcular o coeficiente de reflexão para polarização paralela ao plano incidente.
c) faça o mesmo para a polarização perpendicular ao plano de incidência.
d) em caso de polarização perpendicular ao plano de incidência, mostre que os campos evanescentes reais são
e) verifique se os campos em (d) satisfazem todas equações de Maxwell.
f) para os campos em (d), construa o vetor de e mostre que, na média, não há transmissão de energia na direção

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Sabendo que,
Temos que na letra (a) para mostrar que,
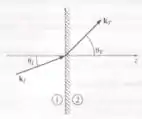
Temos,
Ficando,
Na letra (b) para calcular o coeficiente de reflexão para polarização paralela ao plano de incidência, temos
Ficando,
Na letra ( c ) para calcular a polarização perpendicular ao plano de incidência, temos
Ficando,
Passo 3
Na letra (d) para mostrar os campos evanescentes reais que são,
Temos,
Na letra (e) para verificar se os campos em (d) satisfazem todas a equação de Maxwell, temos
Ficando,
E por fim na letra (f) para construir o vetor de Poynting, temos
Ficando,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a)
b)
c)
d)
e)
f)