Sistema inercial em relação ao sistema A. (O eixo desliza ao longo do eixo x , e as origens coincidem em , como sempre).
(a) Em papel quadriculado, monte um sistema de coordenadas cartesianas com eixos ct e x . Desenhe cuidadosamente as linhas que representam Desenhe também as linhas correspondentes a . Rotule suas linhas claramente
(b) Em, observa-se que uma partícula livre se desloca do ponto o ponto. Indique esse deslocamento em seu gráfico. A partir da inclinação desta linha, determine a velocidade da partícula em S.
(c) Use a regra de adição de velocidade para determinar a velocidade em S algebricamente e verifique se sua resposta é consistente com a solução gráfica em (b).
Passo 1
Salve, Salve nação, tudo belezinha?
Bora resolver essa bomba juntos? Haha
Simboráaaaa
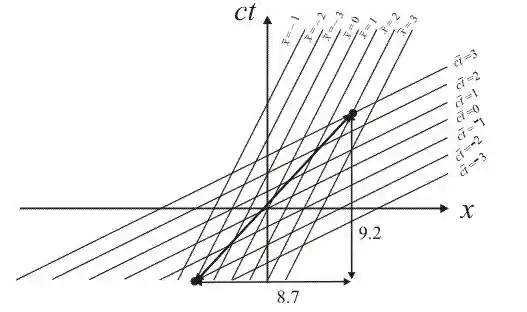
- A figura abaixo mostra o gráfico do sistema de coordenadas cartesianas com eixos ct e x como segue :
- Em paralelo observa-se viajar de ao ponto a inclinação desta linha é
- Temos que se move na direção x com velocidade em em relação ao sistema s
Passo 2
Portanto, a velocidade da partícula em S é .
Passo 3
A velocidade da partícula em relação ao quadro é
Então a velocidade da partícula em relação ao referencial s em
Assim, pela regra da adição de velocidade, a velocidade da partícula no referencial S é igual a velocidade da partícula no referencial S pela solução gráfica.
Resposta
- Gráfico
- Portanto, a velocidade da partícula em S é .
- Assim, pela regra da adição de velocidade, a velocidade da partícula no referencial S é igual a velocidade da partícula no referencial S pela solução gráfica.