O sistema inercial move-se com velocidade constante com relação a S. Seus eixos são paralelos um ao outro e sua origens coincidem em como de costume. Encontre a matriz (equação 12.25)
RESPOSTA:

Passo 1
Faaaaaala, galera... Tranquileba??
Como dito, os eixos são paralelos de forma que o ângulo formado pelo vetor é igual em ambos. Um esboço que representa essa situação é:
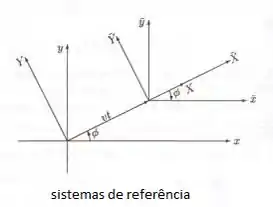
Onde:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Usando a transformação de Lorentz da equação 12.18, temos:
Usando que
Passo 3
Rotacione de para assim:
Assim:
E:
Assim:
Assim temos todas as componentes, isto é: , rearranjando de forma matricial:

Resposta
