Suponha que J ( r ) seja constante no tempo, então ( Prob.7.55 ) . Mostre que
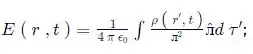
Ou seja, a lei de Coulomb se aplica com a densidade de carga avaliada no tempo não retardado
Passo 1
E ai meus queridos, tudo dentro dos eixos?
Haha
Bora resolver essa comigo?
Encostaaa
Aqui e dado que
é constante no tempo então
Nos sabemos que
Passo 2
Aqui