Usando as definições nas equações 1.1 e 1.4, bem como os diagramas apropriados, mostre que os produtos escalar e vetorial são distributivos,
(a) quando os três vetores são coplanares;
(b) no caso geral.
Passo 1
Faaaala meu povo!! Como vocês estão? Bora lá resolver mais uma questãozinha?
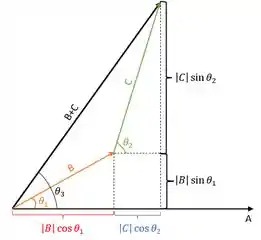
Antes de tudo, vamos desenhar o diagrama do problema dado, para que a gente possa entender melhor o que acontece, e qual caminho devemos seguir para fazer o que o problema está pedindo!
Passo 2
A partir do diagrama, quando os três vetores forem coplanares, podemos afirmar que no caso do produto escalar, teremos:
Agora, se multiplicarmos a expressão acima por , teremos:
Portanto:
Assim, observamos que o produto escalar é distributivo.
Passo 3
Já para o produto vetorial (quando os três vetores forem coplanares), podemos fazer similarmente ao produto escalar, multiplicando por :
Se é o vetor unitário apontando para fora da página, temos que:
Portanto, o produto vetorial também é distributivo.
Passo 4
Já no caso geral, vemos que o diagrama obedece ao produto escalar .
A partir do diagrama, vemos que isso é o mesmo que: , e é, portanto, distributivo.
Ainda falando do caso geral, mas no caso do produto vetorial, vemos que: devido ao vetor unitário que aponta para fora da página. Vemos que este caso é o mesmo descrito no passo 2, e, portanto, é distributivo.
Por essa questão é isso galerinha, bora pra mais uma?
Resposta
a. – distributivo
b. - distributivo