Use a lei de Gauss para encontrar o campo elétrico dentro de uma esfera uniformemente carregada (com densidade de carga ). Compare sua resposta ao problema 2.8.
Passo 1
Falaaa, tudo belezaa?? Para acharmos o campo elétrico com a lei de Gauss usamos a fórmula abaixo:
Quer dizer que a integral do campo elétrico em uma superfície fechada é igual a carga envolvida dividida por uma constante. O que precisamos agora é definir a superfície e a carga envolvida. Bora lá!!!
Passo 2
A esfera pode ser analisada abaixo:
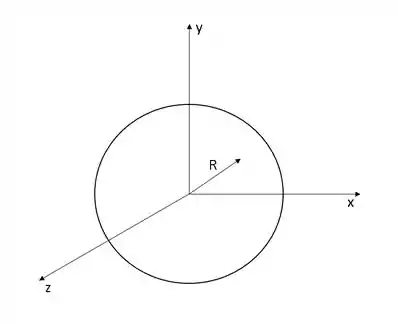
Para encontrarmos o campo elétrico onde , ou seja, a superfície de Gauss é menor que o raio da esfera. Lembrando, que este exercício difere do Problema 2.11, pois a esfera é maciça agora.
Então, agora teremos carga envolvida em . E está carga como a densidade de carga é uniforme será . Onde é o volume da esfera envolvido pela superfície Gaussiana e a superfície continua sendo como no problema 2.11.
Substituindo os valores:
A diferença que acontece na resposta do Problema 2.8, é que aqui o campo elétrico depende somente do raio da superfície Gaussiana e não depende do raio da esfera.