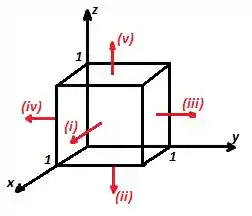
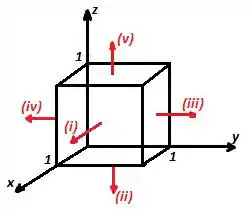
Verifique o Corolário 1 usando a mesma função e a mesma linha de contorno do Exemplo 1.11, mas calculando a integral sobre os cinco lados do cubo da figura 1.35. A face de trás do cubo é aberta.
Passo 1
Vamos lá. Temos a seguinte função:
De acordo com o Corolário 1, temos:
Então, temos que:
Passo 2
Para a integral de linha, vamos considerar os cincos segmentos:
Para :
Para :
Para :
Para :
Para :
Então, somando os cinco segmentos teremos:
Resposta
Assim verificamos o Corolário 1 para a função usando a figura dada. Ficou claro?