Admita que as linhas de corrente dos vórtices posicionados nas pontas das asas dos aviões podem ser consideradas circulares e que a velocidade desses escoamentos é dada por , onde K é uma constante. Determine a aceleração na direção da linha de corrente , e a aceleração normal desses escoamentos.
Passo 1
Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão desse assunto!
Lá do problema anterior e dessa situação em geral, a gente tem as seguintes igualdades pras componentes da aceleração:
Da ilustração a seguir, notamos que .
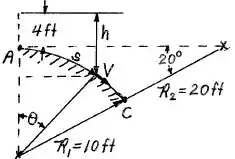
Logo:
Isso nos dá que:
Esse resultado é válido para um ângulo entre 0 e .
Resposta
Esse resultado é válido para um ângulo entre 0 e .