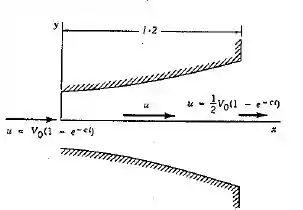
Água escoa pelo difusor mostrado na Fig. P4.23 quando uma válvula é aberta. A velocidade ao longo da linha de centro do difusor é dada, em função do tempo, por onde u, c e l são constantes. Determine a aceleração do escoamento em função de x e t. Se Vo=3,0 m/s e l=1,5 m, qual o valor de c (não nulo) necessário para que a aceleração seja nula em qualquer x e em t=2s? Como a aceleração pode ser nula num escoamento onde a vazão em volume aumenta com o tempo?
Passo 1
Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão desse assunto!
Para essa situação, o que vai valer é a seguinte equação de aceleração:
Como “u” expresso na equação trazida do enunciado, transformamos essa equação em:
Passo 2
Usando essa equação para um para qualquer X ao tempo de 1 s, nós teremos que:
A raiz dessa última equação é igual a .