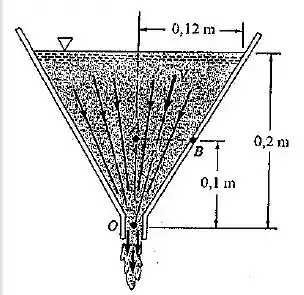
Água escoa em regime permanente no funil mostrado na Fig. P4.45. O escoamento em funil pode ser considerado radial, com centro em O, na maior parte do tempo do escoamento. Nesta condição é possível admitir que , onde r é a coordenada radial e c uma constante. Determine a aceleração nos pontos A e B sabendo que a velocidade é igual a 0,4 m/s quando r=0,1 m.
Passo 1
Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão desse assunto!
Escrevendo o vetor aceleração, a gente tem o seguinte com as duas coordenadas:
Também temos que cada coordenada se determina assim:
A questão nos fala que .
Então, se nós temos que quando , podemos determinar c:
Logo, podemos escrever a coordenada na direção da linha da seguinte maneira:
Passo 2
Logo, pro ponto A vamos ter:
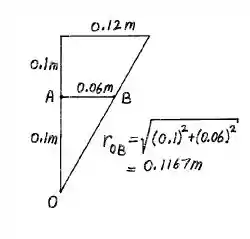
Para o ponto B, podemos descobrir o valor de r aplicando regra simples da trigonometria como mostra a ilustração abaixo:
Resposta
Ponto A:
Ponto B: