Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 4.Problemas - Ex. 44
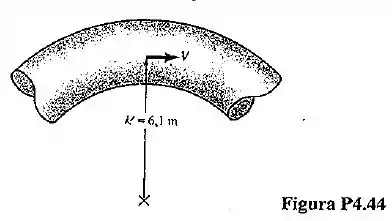
A água escoa na tubulação curva mostrada na Fig. 4.44. A velocidade do escoamento é dada por , onde t é medido em s. Admitindo que , determine (a) o componente do vetor aceleração na direção da linha de corrente, (b) o componente do vetor aceleração na direção normal à linha de corrente, e (c) o módulo, direção e sentido do vetor aceleração deste escoamento.
Passo 1
Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão desse assunto!
- Pra direção da linha de corrente, a gente vai ter a seguinte componente de aceleração:
- Na componente normal à linha de corrente, vamos ter essa relação já conhecida por nós:
- Quando a aceleração for no tempo , vamos ter que o vetor vai ficar:
Más nós sabemos que . Com isso, vamos ter a seguinte resposta:
Para o tempo dado no enunciado teremos:
Passo 2
Ou seja:
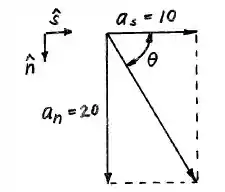
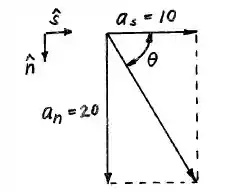
A figura a seguir ilustra o sentido e direção do vetor, porém com acelerações em :
Resposta
