Aplique a lei de conservação da massa a um elemento em um sistema de coordenadas polares e obtenha a equação da continuidade para um escoamento estacionário, bidimensional e incompressível.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
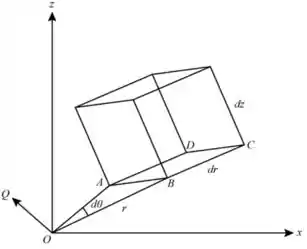
A figura abaixo mostra um esquemático de controle de volume 2D para um escoamento incompressível e permanente
Passo 2
Para o diagrama mostrado:
De acordo com a lei de conservação de massa:
Aqui, o fluxo de massa em cada face do controle de volume é e o passo de tempo da mudança de massa dentro do volume de controle é
Passo 3
O ganho total na massa deve ser igual a taxa de mudança da massa do fluido no elemento e é dado por:
Mas é sabido que para um escoamento permanente , então:
Passo 4
Para um escoamento incompressível,
Então a equação da continuidade em coordenadas polar para um escoamento permanente e incompressível