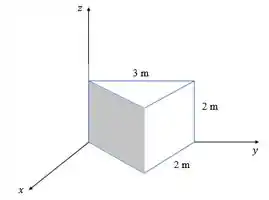
A área sombreada mostrada está num escoamento onde o campo de velocidade é dado por , e . Escreva uma expressão vetorial para o elemento da área sombreada. Avalie as integrais e sobre a área sombreada.
Passo 1
Vamos lá! Nessa questão temos um campo de velocidade e a geometria do volume de controle. Precisamos encontrar a taxa de fluxo de volume e fluxo de momento . O nosso ponto inicial, então, é definir os vetores de área e velocidade.
ou
Pelas equações da superfície: ou . Então,
Assim,
Passo 2
Para o fluxo de momento, temos:
Assim,
Da superfície, nós temos que ou . Além disso, e . Então,
Resolvendo a integral,
Substituindo , e , a expressão vetorial é dada por: