Um bloco com dimensões de pesando deve ser deslocado com a velocidade constante de num plano inclinado com o coeficiente de atrito . Determine a força que precisa ser aplicada na direção horizontal. Se uma película de óleo de de espessura com viscosidade dinâmica de for aplicada entre o bloco e o plano inclinado, determine o porcentual de redução na força requerido.
Passo 1
Falaaaaa galerinhaaa bonita!
Aqui nessa questão, a gente tem um caso clássico de bloco no plano inclinado. O enunciado diz que a velocidade é constante, então isso significa que a aceleração é zero e o sistema está em equilíbrio.
E quem vai fazer esse equilíbrio acontecer é uma força horizontal aplicada sobre o bloco. E o que a gente quer é justamente encontrar essa força.
Mas a gente tem duas situações diferentes pra avaliar.
- No primeiro caso, temos atrito entre o bloco e o plano.
- No segundo caso, temos uma película de óleo com viscosidade dinâmica e espessura conhecidas.
E agora? Como resolver?
O primeiro caso é mais básico né minha gente. Temos nossas forcinhas de sempre atuando (peso, normal, atrito e a força horizontal). E como o sistema ta em equilíbrio, podemos fazer o somatório de forças igual a zero nas duas direções e assim achar .
No segundo caso, você vai precisa relembrar de alguns conceitos de tensão de cisalhamento!!! Tá lembrado? Bora lá!
A película de óleo vai causar uma tensão de cisalhamento entre o plano e bloco, que também vai atuar como uma resistência ao movimento. Ou seja, a força de cisalhamento, resultante dessa tensão, também vai se opor ao movimento relativo entre as superfícies, então ela vai ter a mesma direção e sentido da força de atrito.
A força de cisalhamento é o produto da tensão de cisalhamento pela área de contato entre o fluido e bloco:
E a tensão de cisalhamento vai depender da viscosidade dinâmica , a velocidade do bloco e a espessura da camada de fluido , a partir da seguinte fórmula:
Então no fim das contas os dois casos vão ser muito parecidos em termos de contas. O que muda é que a força de cisalhamento vai entrar “no lugar” da força de atrito e, logicamente, como calcula cada uma delas.
Bora fazer conta!
Passo 2
O primeiro caso, é o que temos atrito entre o bloco e a superfície, então o DCL fica assim:
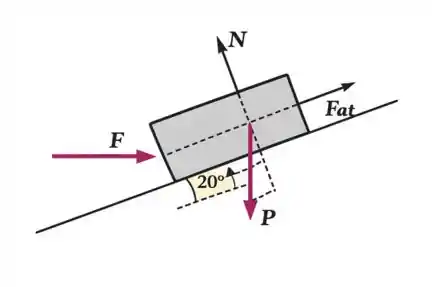
Como temos equilíbrio, então o somatório de forças é zero nas duas dimensões.
:
:
Sendo que:
Substituindo os valores nas duas equações:
Da segunda equação, conseguimos a força normal:
E substituindo na primeira obtemos o valor da força que deixa todo esse sistema em equilíbrio:
Terminamos o primeiro caso. Agora vamos avaliar o que acontece quando entra aquela película de óleo.
Passo 3
No segundo caso, a força de atrito é substituída pela força de cisalhamento, que, como vimos no passo 1, é dada por:
Em que:
- é a espessura do fluido
- é a viscosidade dinâmica
- é a velocidade do bloco
Já a superfície de contato tem dimensões por , então sua área é:
Substituindo os valores, achamos a tensão de cisalhamento:
E a força de cisalhamento:
Passo 4
Agora vamos analisar o sistema de novo. Como vimos no passo 1, a força de cisalhamento atua muito parecido com a força de atrito, pelo menos em termos de direção e sentido. Então o DCL fica assim:
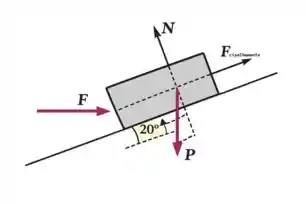
Mais uma vez, podemos fazer os somatórios de forças iguais a zero.
:
:
Substituindo os valores nas duas equações:
Da segunda equação, conseguimos a força normal:
E substituindo na primeira obtemos o valor da força que deixa todo esse sistema em equilíbrio:
Passo 5
Por fim, temos que a redução percentual da força requerida será:
Entendeu tudo? Respira fundo e bora continuar!
Resposta
Portanto temos que,
A força que precisa ser aplicada na direção horizontal é:
O porcentual de redução na força requerida é: