Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 96
O que é camada limite de concentração? Como ela é definida para escoamento sobre placa?
Passo 1
Antes de responder vamos retomar o conceito de camada limite. Camada limite é uma região de fluido que é afetada pela presença de uma superfície. Por exemplo, no caso de uma camada limite térmica se temos uma corrente de ar frio escoando sobre uma superfície quente, o ar próximo à superfície será aquecido devido à diferença de temperatura. A região de ar que é aquecida chamamos de camada limite térmica. Vamos agora aplicar este conceito para definir a camada limite de concentração.
Passo 2
Imagine uma corrente de ar seco escoando sobre uma piscina:
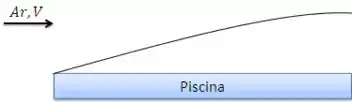
Como o ar é seco (fração de água é zero) e a piscina está cheia de água, há um gradiente de concentração. A região em que ocorre a formação do gradiente de concentração chamamos de camada limite de concentração.
Passo 3
Para o escoamento sobre placa plana só precisamos adaptar o exemplo da piscina e imaginar que temos uma superfície plana, em que a camada de fluido está saturada com o composto. Da mesma forma, será formada uma camada limite de concentração, desde que haja um gradiente de concentração entre o fluido e que escoa e a camada em contato com a superfície.
Resposta
Ei, a resposta está no passo a passo :)