O campo de velocidade de um escoamento é dado por Onde y são medidos em metros. Determine a velocidade do fluido ao longo dos eixos e Quais são os ângulos formados pelos vetores velocidade com o eixo nos pontos ?
Passo 1
Opa galerinha boa, como vocês tão? Certinho? Pois bora pra questão! Aqui ela tá pedindo pra gente calcular a velocidade do fluido e os ângulos para três pontos diferentes. Bem parecida com a questão 4.1, portanto eu aconselho vocês darem uma olhadinha nela só pra ajudar a contextualizar, fechado? Bora continuar então. Transcrevendo em outras variáveis, temos:
Passo 2
Agora que a gente tem as cartas na mesa, bora organizar as coisas e encontrar o que a questão nos pede! Saca só: A gente sabe que a velocidade pra esse caso é dada por:
Então é só a gente aplicar para os dois casos que a questão deu pra gente e depois calcular o ângulo. Temos, aplicando as variáveis e , o seguinte:
Fazendo um joguinho de álgebra, temos:
Para qualquer ponto! Agora a bronca são os ângulos... vamo pro próximo passo.
Passo 3
Pro ângulo entre os vetores velocidade e os pontos, temos:
Ou,
Logo, para os casos temos:
(5,0);
(5,5);
(0,5);
Fica mais ou menos assim o esquema:
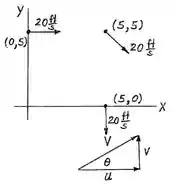
E é isso! Pode parecer impossível no começo mas no desenvolvimento a gente vê que é simples 😊 Até a próxima questão, meus bacanos
Resposta
(5,0);
(5,5);
(0,5);