Para o caso de uma camada-limite turbulenta sobre uma placa plana, mostrou-se que o perfil de velocidades segue muito bem a forma:
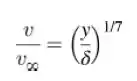
Considerando um perfil de temperaturas da mesma forma, ou seja,
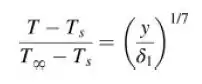
e supondo que δ = δ1, use a relação integral para a camada-limite de modo a obter hx e Nux. O gradiente de temperatura na
superfície pode ser considerado similar ao gradiente de velocidade em y = 0, dado pela equação (13-26).
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transferência de calor por convecção!
Trabalhando com a equação de energia, temos que:
Passo 2
Resolvendo os dois lados dessa integral e presumindo que para fins de integração temos que:
E por fim: