Ar, na condição padrão, escoa ao longo de uma placa plana. A velocidade da corrente livre, não perturbada, é . Em , a jusante da borda de ataque da placa, a espessura da camada limite é . O perfil de velocidade nesse local é
Calcule a componente horizontal da força por unidade de largura requerida para manter a placa estacionária.
Passo 1
Vamos lá! A questão nos deu um escoamento com velocidade na camada limite com e . Ela nos deu também o perfil de velocidades e pediu a força na placa por unidade de comprimento.
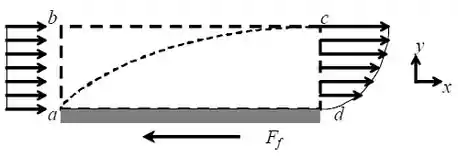
Para isso, vamos usar a equação da continuidade e quantidade de movimento na direção :
E
Passo 2
Da equação da continuidade, temos:
Onde é o fluxo mássico escoando por (na figura).
Assim,
Passo 3
Agora pela equação da quantidade de movimento em , temos que a força de arrasto é dada por:
Então, a força de arrasto é
Passo 4
O enunciado nos deu o perfil de velocidades
Vamos chamar . Assim,
Substituindo na equação da força de arrasto por unidade de comprimento, conforme o passo 3, temos:
Substituindo o perfil de velocidades:
Assim, usando o valor da densidade atmosférica padrão e fazendo as conversões de unidade, temos: