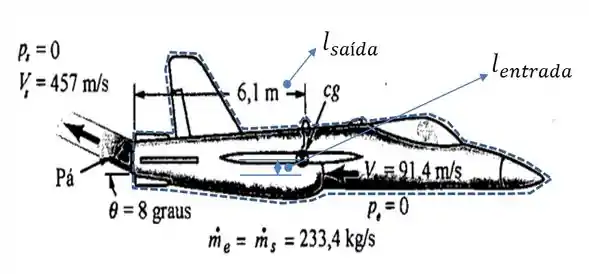
O controle vetorial de propulsão é uma técnica que pode melhora substancialmente a manobrabilidade dos aviões de caça. Esta técnica é baseada no controle dos jatos descarregados das turbinas dos aviões através de pás defletoras instaladas nas seções de descarga dos jatos (a) Considere as condições operacionais indicadas na Fig P5.35. Determine o momento de “pitch” (o momento que faz o nariz do avião subir) em relação ao centro de massa do avião (b) Compare o empuxo associado às condições operacionais indicadas na figura e aquele associado à situação onde o jato é descarregado paralelamente à linha de centro do avião.
Passo 1
E aí, galerinha! Oia nós aqui de novo!
Mais um exercício de conservação de massa!
Vamos começar fazendo um esboço do volume de controle e destacando os aspectos mais importantes do nosso sistema:
Dessa forma, aplicando a fórmula da conservação de massa ao longo do volume de controle, temos que...
E quando a gente tá falando em volume de controle e conservação de massa... Considerando o nosso escoamento como incompressível, temos que a vazão vai ser a mesma ao longo de todo o fluxo do líquido...
Passo 2
Assim, aplicando a equação de momento perpendicularmente ao plano de onde estamos vendo o avião, temos que...
Como pela figura, substituindo os valores numéricos...
Passo 3
E aplicando também a fórmula do impulso, temos que:
Rearranjando, temos que...
Passo 4
Assim, substituindo os valores numéricos, obtemos nossa resposta:
Resposta
a)
b)