Deduza a expressão para a distribuição de velocidades e para a queda de pressão para um fluido newtoniano em escoamento laminar completamente estabelecido no espaço anular entre dois tubos concêntricos horizontais. Aplique o teorema do momento para uma casca anular de fluido de espessura Δr e mostre que a análise de tal volume de controle conduz a
As expressões desejadas podem ser então obtidas pela substituição da lei de Newton da viscosidade e duas integrações.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Desenhando o controle de volume do cilindro tendo um raio interno , espessura e comprimento :
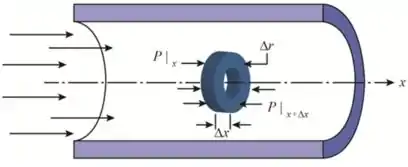
Passo 2
Usando a expressão para o volume de controle para um momento linear na direção para derivar o resultado:
A força total no elemento é dada por:
Aqui, representa a pressão e representa a tensão de cisalhamento no fluido.
Para um escoamento permanente e totalmente desenvolvido:
E
Passo 3
Substituindo:
E o valor de na Equação (1):
Dividindo ambos os lados da equação por :
Como o volume de controle se aproxima de um tamanho diferencial, e se aproximam de zero, a equação se torna:
Passo 4
Rearranjando a última equação do Passo 3:
Integrando a equação acima e inserindo os limites de a para e à para
Passo 5
Para determinar a distribuição de velocidade, integramos a equação do Passo 4
Aqui, é uma constante de integração.
Passo 6
Para um escoamento laminar em fluido newtoniano, a tensão de cisalhamento é dada por
Aqui, temos:
1. viscosidade do fluido,
2. velocidade do fluido na direção ,
3. distância do centro do tubo,
Substituindo :
Integrando a equação acima para obter a expressão de
Aqui, é a constante de integração.
Passo 7
Agora considerando um fluido de casca anelar de espessura onde
O raio exterior da casca é e o raio interno da casca é
Aplicando as condições de fronteira para determinar os valores de constantes e :
Em , a velocidade é zero, que é,
Substituindo e :
Em , velocidade é zero,
Resolvendo as equações obtidas para e
Passo 8
Substituindo os valores de e para obter uma distribuição de velocidade para a casca: