Deseja-se concentrar a espécie A a partir de uma mistura de solutos A e B dissolvidos em água, empregando-se uma membrana porosa. A membrana contém poros cilíndricos em arranjo paralelo e uniforme. O fator de separação (α) é definido por:
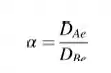
A massa molar do soluto A é 142 g/gmol, o diâmetro molecular é 2,0 nm e o volume molar no ponto de ebulição é 233,7 cm3/gmol. A massa molar do soluto B é 212 g/gmol, o diâmetro molecular é 3,0 nm e o volume molar no ponto de ebulição é 347,4 cm3/gmol.
- Estime os coeficientes de difusão dos solutos A e B em água a 293 K em diluição infinita.
- Determine o diâmetro de poro (dporo, em nanômetros) que permite a separação com fator α = 3 para esse processo.
Sugestão: uma solução interativa do tipo tentativa e erro será requerida.
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transferência de calor e seus fundamentos!
- Vamos juntar os dados que temos:
- Usando a equação 24.33, temos que:
Agora podemos trabalhar com as fórmulas dadas no capítulo.
Ou seja:
Passo 2
Nós temos que:
Substituindo, chegamos que .
Usando a equação 24.58, temos finalmente que: