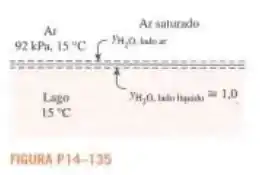
Determine a fração molar do vapor de água na superfície de um lago cuja temperatura é e compare-a com a fração molar da água no lago. Considere a pressão atmosférica ao nível do lago igual a .
Passo 1
Dados fornecidos:
Temperatura do lago:
Pressão atmosférica:
Premissas:
1) O vapor de ar e de água são gases ideais.
2) O ar é fracamente solúvel em água e, portanto, a lei de Henry é aplicável.
Passo 2
Podemos obter a pressão de saturação da água a na Tabela A-9.
Pressão de saturação da água:
Análise O ar na superfície da água será saturado. Portanto, a pressão parcial do vapor de água no ar na superfície do lago será simplesmente a pressão de saturação da água a .
Passo 3
Podemos assumir que o ar e o vapor sejam gases ideais, assim, a fração molar do vapor de água no ar na superfície do lago é determinada pela Eq. 14-11. Assim temos:
Substituindo os termos da equação pelos dados obtidos, temos:
Passo 4
A água contém um pouco de ar dissolvido, mas a quantidade é insignificante. Portanto, podemos assumir que todo o lago é água líquida. Então sua fração molar se torna:
Discussão: Observe que a concentração de água em uma base molar é abaixo da interface ar-água e acima dela, mesmo que se presuma que o ar esteja saturado (portanto, esse é o valor mais alto a ). Portanto, enormes descontinuidades podem ocorrer nas concentrações de uma espécie através dos limites das fases.