Determine os módulos e os sentidos das componentes nas direções e da força necessária para imobilizar o conjunto cotovelo-bocal esboçado na fig . O conjunto está montado na horizontal. Determine também os módulos e sentidos das componentes das forças exercidas pelo cotovelo e pelo bocal sobre o escoamento da água.
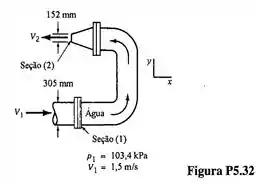
Passo 1
E aí, galerinha! Oia nós aqui de novo!
Mais um exercício de conservação de massa!
Vamos começar fazendo um esboço, delimitando o volume de controle e destacando as forças atuantes nesse sistema...
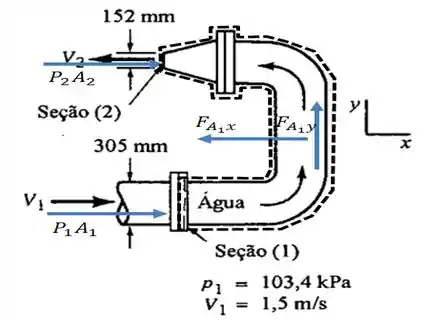
Dessa forma, aplicando a fórmula da conservação de massa ao longo do volume de controle, temos que...
E quando a gente tá falando em volume de controle e conservação de massa... Considerando o nosso escoamento como incompressível, temos que a vazão vai ser a mesma ao longo de todo o fluxo do líquido...
Passo 2
Assim, aplicando o somatório das forças na direção vertical, em relação à , temos que...
E depois, aplicando o somatório das forças na direção horizontal, em relação à , temos que...
Pela equação de conservação de massa, temos que...
Então, a equação anterior fica assim...
Isolando :
E substituindo os valore numéricos, obtemos que...
Passo 3
Com base nisso, como :
E uma vez, que pelo teorema da continuidade...
Então,