Um elemento cilíndrico combustível nuclear tem 10,16 cm de comprimento e 10,77 cm de diâmetro. O combustível gera calor uniformemente a uma taxa de 51,7 × 103 kJ/s × m3 . O combustível é colocado em um ambiente com uma temperatura de 360 K e um coeficiente de transferência de calor de 4540 W/m2 · K. O material combustível tem k = 33,9 W/m · K. Para a solução descrita, calcule o seguinte, em estado estacionário: o perfil de temperaturas como função da posição radial a temperatura máxima do combustível a temperatura da superfície Efeitos de extremidade podem ser desprezados
Passo 1
Opa galerinha, beleza com vocês?! Então bora lá pra cima dessa questão! Da formula padrão para a velocidade tangencial de um cilindro, temos que:
Para um valor de pequeno, temos essa taxa de mudança na velocidade do fluido:
E a tensão de cisalhamento entre os cilindros é dada por:
A força de cisalhamento é:
E por fim, o torque desenvolvido é:
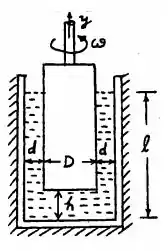
Passo 2
Agora que temos as formulas que vamos usar na questão, vamos por a mão na massa! Para um pequeno, a taxa de mudança de velocidade do fluido em uma direção vertical é:
Tensão de cisalhamento para esse caso:
Força em uma área .
Passo 3
A partir disso, o torque entre as superfícies inferiores do cilindro é dada por:
Onde,
Logo,
Portanto, o torque final é dado por:
Passo 4
Expressando como v:
Temos uma constante de amortecimento: