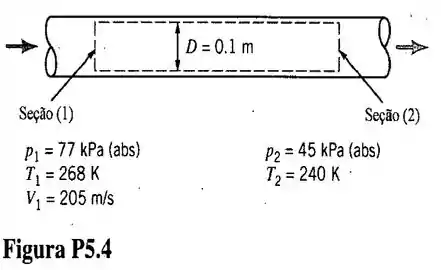
Ar escoa em regime permanente ao longo do tubo mostrado na fig . Levando em consideração as pressões estáticas e temperaturas estáticas indicadas na figura, determine a velocidade média na seção (2) sabendo que a velocidade média de escoamento na seção (1) é igual a .
Passo 1
E aí, galerinha!
Bora lá, pra mais um exerciozinho aew!
Pois muito bem! Pra essa questão, temos que determinar a velocidade média na seção (2) sabendo que a velocidade média de escoamento na seção (1) é de .
Então galera, esse é um exercício onde devemos calcular o balanço de água que entra sendo igual ao balanço de água que sai, ou seja!
E considerando então, o fluido como incompressível, isto é, sem mudança na vazão... Temos que:
Onde...
Passo 2
Mas a gente não sabe nada dessas densidades aew!
Como que a gente vai proceder então?
Ora bolas! Vamos considerar o ar como gás perfeito! Sendo assim, usando a lei dos gases, temos que...
Isolando , que é um termo que não muda...
Dessa forma, temos que...
Combinando então as equações e , e isolando , que é o que queremos encontrar, obtemos que...
Como a área da seção transversal é igual (), então...
Assim, substituindo os valores numéricos...
Pronto! Finalizamos aqui!