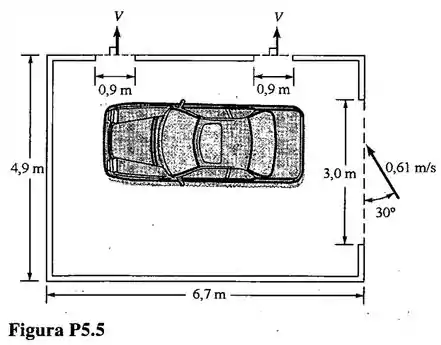
Ar escoa com velocidade de na porta da garagem esboçada na fig. (a altura da porta é igual a ). Determine a velocidade média dos escoamentos nas duas janelas indicadas na figura, , sabendo que as alturas das janelas são iguais a .
Passo 1
E aí, galerinha! Simbora pro nosso quinto exercício aí sobre volumes de controle!
Então galera, esse é um exercício onde devemos calcular o balanço de água que entra sendo igual ao balanço de água que sai, ou seja!
E quando a gente tá falando balanço é sobre “vazão”. Considerando o nosso escoamento como incompressível, temos que a vazão vai ser a mesma ao longo de todo o fluxo do líquido...
Passo 2
Dessa forma, temos que...
Sabendo então, que...
A velocidade nas duas janelas são a mesma, isto é...
E sabendo também que a área dessas duas janelas é um retângulo de e que a área da porta da garagem é um retângulo de , então temos que...
Isolando ...
Essa é a velocidade que incide horizontalmente. Como o ar escoa com velocidade de a , logo obtemos que...
Essa é a velocidade média dos escoamentos nas duas janelas