Para um escoamento bidimensional e incompressível, com velocidade υx = υx(y), esquematize um elemento de fluido tridimensional e ilustre a magnitude, a direção e a superfície de ação de cada componente de tensão.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
A figura abaixo mostra um elemento de fluido tridimensional. Todas essas forças com suas direções:
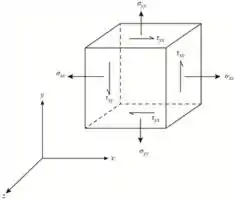
Na figura a gente tem:
1. força normal na direção ,
2. força normal na direção ,
3. força cisalhante no plano normal ao eixo e na direção ,
4. força cisalhante no plano normal ao eixo e na direção ,
Passo 2
O escoamento é bidimensional, que é somente nas direções e
É dado que a velocidade de escoamento,
Velocidade de escoamento na direção ,
Tensão normal na direção ,
Já que então
Passo 3
Tensão de cisalhamento agindo no plano normal ao eixo e na direção é
Então os valores de e são dependentes de que é igual a
Tensão de cisalhamento agindo no plano normal ao eixo e na direção é
Então os valores de e são dependentes de que é igual a