Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 10
Explique como a forma das diferenças finitas do problema de condução de calor é obtida pelo método do balanço de energia.
Passo 1
O método de balanço de energia se baseia na subdivisão do meio em número de elemento suficiente de elementos de volume e, em seguida, na aplicação do balanço de energia em cada elemento.
Passo 2
Podemos supor que uma parede plana de expessura . Com ocorrência transferência de calor unidimensional permanente.
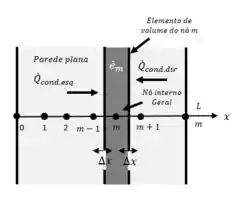
Agora vamos considerar que a nossa parede plana possua uma geração de calor e condutividade térmica constante . E que esteja dividida em regiões iguais de espessura = na direção .
Passo 3
Para obtermos a quação geral de diferenças finitas para os nós internos, o balanço de energia pode ser expressado como:
Ou
Sob condições permanente temos que...
A taxa de geração de calor dentro do elemento pode ser expressa como:
Onde é a taxa de geração de calor por unidade de volume em .
Passo 4
Temos que para taxa de condução de calor pode ser expressa como:
Resposta
Para finalizar basta susbstituirmos nossas equações encontradas em nossa primeira equação geral...
A propriedade do nosso nó, como a temperatura e a taxa de geração de calor, representa as propriedades médias do elemento é como se a temperatura variasse linearmente de um nó para outro.