A extremidade aberta de um tanque cilíndrico de 2 ft de diâmetro e 3 ft de altura está submersa em água, conforme mostrado. Se o tanque pesa 250 lb, até que profundidade h o tanque irá submergir? A pressão barométrica do ar é 14,7 psia. A espessura da parede do tanque pode ser desprezada. Que força adicional é requerida para igualar o topo do tanque com a superfície da água?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Desenhando o tanque cilíndrico submergido:
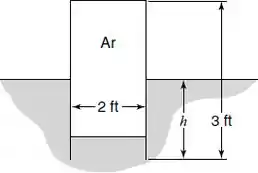
Passo 2
Calculando a área do tanque:
Aqui, o diâmetro do cilindro é .
Substituindo para na equação:
Passo 3
Escrevendo a expressão para a pressão total no nível da água dentro do tanque cilíndrico submergido
Aqui, a pressão atmosférica do ar é , a densidade da água é , a aceleração da gravidade é e a altura onde o tanque está submerso na água é .
O peso do tanque é
O peso da água deslocada é
Passo 4
Considerando o princípio de Arquimedes, o peso do tanque cilíndrico deve ser igual ao peso da água deslocada
Substituindo valores na equação:
Passo 5
Substituindo o valor encontrado para na equação obtida no começo do Passo 3:
Para compressão isotérmica do ar:
Aqui, o volume inicial do tanque é , volume do ar no tanque depois dele submerso na água é , o peso total do cilindro é
Substituindo os dados que temos
Substituindo para
Substituindo o valor de na equação obtida no Passo 4
Passo 6
Desenhando o diagrama mostrando o topo do tanque cilíndrico tocando o nível da água depois da aplicação da força
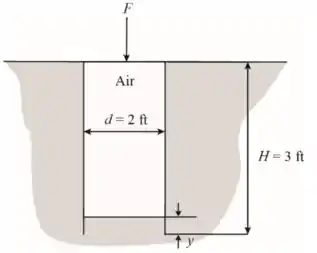
Escrevendo a expressão para a pressão total no nível da água dentro do cilindro totalmente submerso:
Expressando a equação da pressão do lado da água:
Das duas equações, temos:
Passo 7
Calculando o valor de da relação da compressão isotérmica do ar
Substituindo na equação obtida no final do Passo 6