Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 5.Problemas - Ex. 19

A fig P 5.19 mostra a vista lateral da região de entrada de um canal que apresentava largura igual a 0,91   m . Observe que o perfil de velocidade na seção de entrada do canal é uniforme e que, ao longe, o perfil de velocidade é dado por u = 4 y - 2 y 2 , onde u está especificado em m / s e y em m . Nestas condições, determine o valor de V :

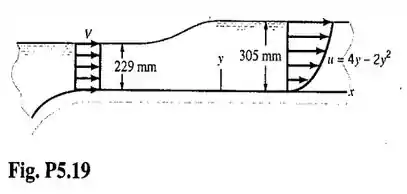
Passo 1

Bom! Bora pra luta, meus queridos!

Vimos na teoria que para um volume de controle, o que entra tem que ser igual ao que sai.

Assim, usando a fórmula da conservação de massa...

Q e n t r a d a = Q s a í d a

Passo 2

Quando o fluido entra, ele passa por uma parte do canal com altura de 229   m m   e largura b . E quando ele sai passa por uma parte com largura b e 305   m m de altura. Só que dessa vez, o perfil é diferente...

Temos então, com base nisso...

V e n t r a d a A e n t r a d a = ∫ s a í d a u d A

V e n t r a d a A e n t r a d a = ∫ 0 0,305 0,91 4 y - 2 y 2 b d y

V e n t r a d a 0,229 b = ∫ 0 0,305 0,91 4 y - 2 y 2 b d y

V e n t r a d a 0,229 b = 0,91 b 2 y 2 - 2 y 3 3 0 0,305

V e n t r a d a 0,229 b = 0 , 152 b

V e n t r a d a = 0,152 0,229

V e n t r a d a = 0,664   m / s

Resposta

V e n t r a d a = 0,664   m / s