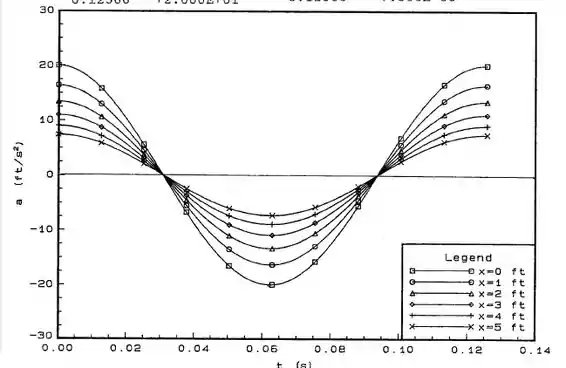
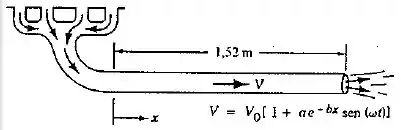
A Fig. P4.33 mostra que a velocidade de exaustão num escapamento automotivo varia com o tempo e com a posição no cano de descarga (devido a amortecimentos que ocorrem nesta tubulação). Admita que o campo de velocidade é o mstrado na figura e que . Calcule e faça um gráfico da aceleração do fluido em para .
Passo 1
Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão que envolve programa computacional na sua resolução!
Como nessa questão, se cumpre também aqueles requisitos de , então a gente pode escrever a aceleração como:
Juntando isso com a equação de velocidade trazida na figura, vamos ter que:
Ou seja:
Agora é preciso atenção pois os dados utilizados daqui em diante e no programa seguirão valendo o mesmo, porém a unidade de comprimento em vez de metro será pés. Teremos então . A equação da aceleração se torna:
Passo 2
Para os dados de e com o mesmo intervalo de tempo, obtemos os seguintes dados no programa P4#33:


E então pode se montar o gráfico pedido na questão.
Resposta