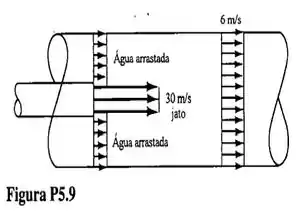
A Figura mostra o esboço de um ejetor líquido-líquido. A área da seção transversal do jato d’água é igual a e a velocidade média do jato é . Este jato provoca o arrastamento de água que, inicialmente, escoa pela seção anular do tubo (veja a figura). A área da seção transversal do tubo é igual a . Determine a vazão de água que é arrastada pelo jato sabendo que a velocidade do escoamento no tubo é uniforme e igual a a jusante do ponto de descarga do jato.
Passo 1
Bom! Mais uma aí, galera!
Vimos na teoria que em escoamento incompressível e permanente o que entra tem que ser igual ao que sai, pois o volume do nosso sistema é fixo e nosso fluido é incompressível.
Assim tudo que entra é igual a tudo que sai:
A gente sabe que o fluido entra em com uma velocidade de e supostamente entra também em com uma velocidade que a gente não sabe e sai em com uma velocidade de .
Ou seja, não temos ideia do que está acontecendo em . Então vamos assumir que esta entrando.
Por que eu fiz isso? A gente precisa montar uma equação com entradas e saídas, certo? Então eu preciso supor que ele é entrada ou saída. Se eu acertar minha suposição o valor que eu achar vai ser positivo. Se eu errar ele vai ser negativo. Então vamos lá.
Vamos montar a equação de entradas e saídas:
Substituindo os valores que temos na figura, chegamos em:
Pronto! Encontramos nossa resultado!