A figura adiante mostra o caso de um fluido escoando paralelamente a uma placa plana, em que para uma distância X a partir da borda de entrada, a placa é mantida a uma temperatura constante, Ts, em que Ts > T∞. Admitindo um perfil cúbico para ambas as camadas-limite hidrodinâmicas e térmicas, mostre que a razão das espessuras, ξ, é expressa como:
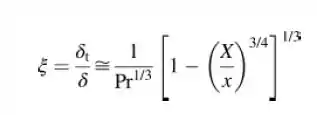
Mostre também que o número de Nusselt local pode ser expresso como:
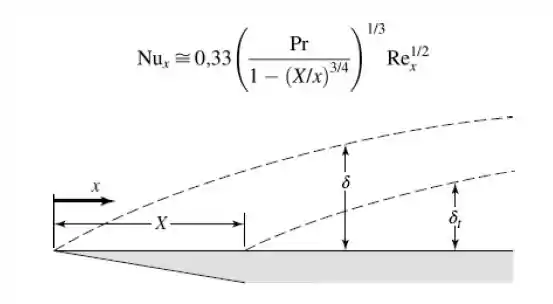
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transferência de calor por convecção!
Bem, assumindo:
Tendo:
O perfil de temperatura se torna: (1)
Da mesma forma pra velocidade: (2)
Passo 2
Desse jeito, a expressão integral fica:
Resolvendo os dois lados dessa equação e substituindo o que foi encontrado nas equações (1) e (2), temos que:
Fazendo:
Teremos que:
Passo 3
Por fim, o número de Nusselt ficaria: