Um jato de ar horizontal com de diâmetro, e axialmente simétrico, atinge um disco estacionário vertical com de diâmetro. A velocidade do jato é na saída do bocal. Um manômetro está conectado ao centro do disco. Calcule (a) a deflexão, , se o líquido do manômetro tem densidade relativa e (b) a força axial exercida pelo jato sobre o disco.
Passo 1
Vamos lá! A questão nos deu um jato de ar atingindo um disco, os diâmetros e a velocidade do jato e ela pede pra gente calcular a deflexão e a força axial.
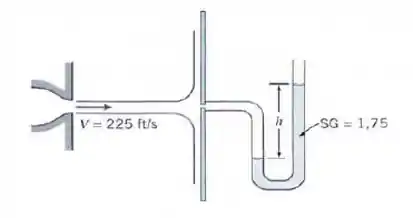
Conforme a figura, beleza? Então vamos precisar da equação de Bernoulli
E da equação do momento na direção :
Vamos por partes!
Passo 2
Primeiro, vamos aplicar a equação de Bernoulli entre a saída do jato e o ponto de estagnação.
Assim,
Mas, sabemos da hidrostática que:
Então,
Substituindo os valores do enunciado e convertendo as unidades, temos:
Passo 3
Agora precisamos da equação momento em para encontrar a força de reação ao jato.
Então,
Assim,
Portanto, a força do jato no disco é e temos: