Uma linha hidráulica de 0,635 cm se rompe repentinamente a 8 m de um reservatório com uma pressão manométrica de 207 kPa. Compare as vazões (em metros cúbicos por segundo) para um escoamento laminar e invíscido a partir de uma linha rompida.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
A figura aqui embaixo mostra o reservatório e a linha hidráulica
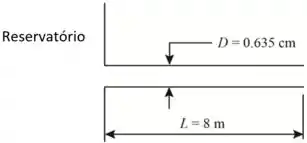
Aplicando a equação de Bernoulli entre o reservatório e a linha de entrada, temos:
Aqui, temos:
1. pressão no reservatório no nível da linha hidráulica,
2. pressão na entrada da linha hidráulica,
3. velocidade do fluido no reservatório,
4. velocidade do fluido na entrada da linha,
5. aceleração da gravidade,
6. diferença no nível do fluido,
Podemos considerar algumas coisas:
1. já que o reservatório e a linha hidráulica estão no mesmo nível,
2. o fluido no reservatório está em repouso,
Então, a equação se torna
Passo 2
Aplicando a equação de Bernoulli entre a entrada e a saída, temos:
Aqui, temos:
1. pressão na entrada da linha hidráulica,
2. pressão na saída da linha hidráulica,
3. velocidade do fluido na entrada da linha,
4. velocidade do fluido na saída da linha,
5. perda devido à atrito,
6. diferença no nível do fluido na entrada e na saída,
Podemos considerar algumas coisas:
1. já que ambas estão no mesmo nível,
2. assumindo que a velocidade do fluido na entrada e na saída da linha hidráulica são iguais,
Então, a equação se torna
Passo 3
Para as condições dadas, a pressão manométrica do reservatório pode ser escrita como
Substituindo o valor de
Já que
Passo 4
Assumindo que o fluido é um fluido hidráulico.
Em , da tabela de propriedades físicas de gases e líquidos:
1. Densidade do fluido hidráulico
Já que
2. viscosidade do fluido hidráulico
Já que
Passo 5
Considerando o caso 1, quando o escoamento através da linha hidráulica é viscoso.
Para um escoamento viscoso, não há atrito entre as diferentes camadas do fluido durante o escoamento.
Então
Substituindo e
Passo 6
Determinando a vazão no escoamento víscido:
Área da linha hidráulica é dada por:
A taxa de vazão é dada por:
Passo 7
Considerando o caso 2, quando o escoamento através da linha hidráulica é laminar.
De acordo com a equação de Hagen-Poiseuille, o gradiente de pressão () é escrito como:
Aqui, temos:
1. viscosidade do fluido hidráulico,
2. velocidade do fluido,
3. diâmetro do tubo,
Para , o gradiente de pressão pode ser escrito como:
Dividindo ambos os lados por
Passo 8
A perda devido ao atrito é dada por:
Substituindo os valores, na equação obtida no Passo 7:
Passo 9
Substituindo valores na equação obtida no final do Passo 3 para achar o valor de
Resolvendo essa equação, temos:
Velocidade nesse caso não pode ser negativa, então:
Passo 10
Determinando a vazão no escoamento laminar:
A taxa de vazão é dada por:
Passo 11
Determinando a razão da taxa do escoamento víscido que o escoamento laminar é: