Um líquido incompressível com viscosidade desprezível e massa específica igual a escoa em regime permanente através de um tubo de de comprimento com seção convergente-divergente, cuja área varia de acordo com a equação
Onde e . Desenvolva uma expressão e trace o gráfico para o gradiente de pressão e para a pressão em função da posição ao longo do tubo, se a velocidade da linha de centro na entrada é e a pressão na entrada é .
Passo 1
Vamos lá! A questão nos deu um escoamento incompressível num tubo com área variável e pediu pra gente expressar a pressão, o gradiente de pressão e plotar. Vamos assumir que o perfil de fluxo permanece inalterado, para que a velocidade da linha central represente a velocidade média e que esse é um escoamento unidirecional.
Usando a equação da continuidade:
Então,
O enunciado fala que a área é dada por:
Então, substituindo:
Passo 2
Para o escoamento dado, a equação para aceleração se reduz a:
Substituindo o valor de , temos:
Para resolver essa derivada, vamos fazer uma substituição e chamar:
Então,
Voltando às variáveis originais:
Jogando na expressão da aceleração:
Então,
Passo 3
Para encontrar o gradiente de pressão vamos usar a equação de Euler:
Simplificando e substituindo a expressão da aceleração que encontramos:
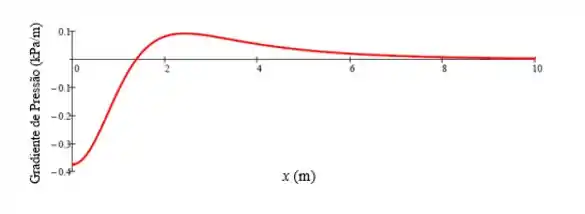
Esse é o nosso gradiente de pressão, agora vamos encontrar quanto vale seu diferencial total.
Passo 4
O diferencial total da pressão é dado por:
Então basta integrarmos a expressão do gradiente de pressão:
Percebe que esta é uma integral muito complexa? Então vamos usar a relação:
Assim,
Então,
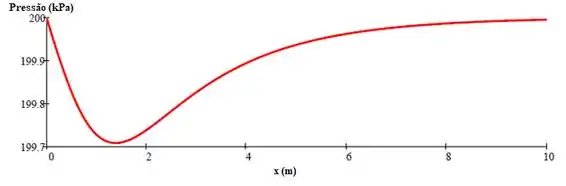
Substituindo :
Chegamos a nossa expressão para , agora podemos plotar os gráficos com os valores dados no enunciado.
Para o gradiente de pressão: