Mostre que a taxa de deformação axial em um escoamento unidimensional, υx = υx(x), é dada por ∂υx/∂x. Qual é a taxa de variação de volume? Generalize para um elemento tridimensional de fluido e determine a taxa de variação de volume.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Considerando um pequeno elemento de fluido de comprimento e largura , na direção
Desenhando a figura que mostra o elemento e a mudança depois de um tempo
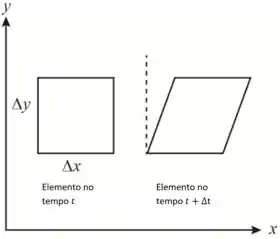
Passo 2
Para um escoamento unidimensional na direção , a velocidade do escoamento é dada por
Para o pequeno elemento de fluido
Então, a tensão axial é dada por
Passo 3
A taxa de tensão axial na direção é dada por
Inserindo o limite , a taxa de tensão axial se torna
Passo 4
Tendo com a área do elemento de fluido na direção
Agora, a taxa de mudança de volume na direção é dada por
Inserindo o limite , a taxa de mudança no volume se torna
Para o resultado obtido, podemos deduzir que ambas as taxas de tensão axial e mudança de volume para um elemento tridimensional são dadas por: