PA11.4 – O sistema da Figura PA11.4 é projetado para fornecer água a 20 °C de um reservatório ao nível do mar para um outro através de um tubo de ferro fundido de 38 cm de diâmetro. As perdas localizadas são ΣK1=0,5 antes da entrada da bomba e ΣK1=7,2 após a saída da bomba.
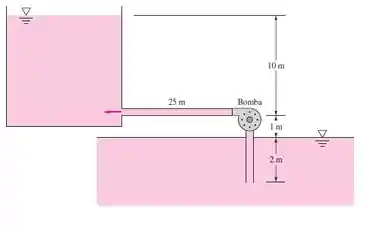
Figura PA11.4
(a) Selecione uma bomba da Figura 11.7a ou 11.7b, operando nas rotações dadas, que possa executar essa tarefa com o máximo rendimento.
Determine (b) a vazão resultante, (c) a potência de eixo e (d) se a bomba neste caso está livre da cavitação.
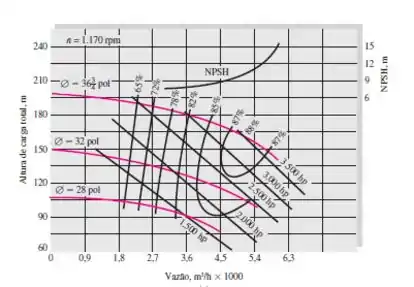
Figura 11.7a
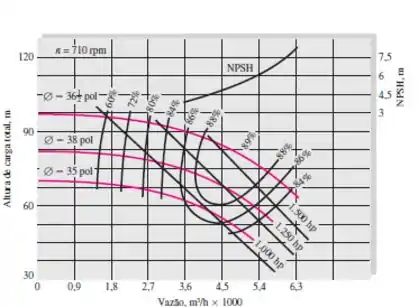
Figura 11.7b
Passo 1
Esta é uma situação prática de encontrar uma bomba para uma determinada aplicação.
Vamos achar o valor da altura de carga e a partir desse valor, usaremos os dados das figuras e faremos uma análise comparativa entre esses dados para ver qual é a melhor bomba, ou seja, com a bomba que atinge o maior rendimento máximo.
Passo 2
Precisaremos encontrar o valor da altura de carga da bomba, H, mas podemos acha-lo pelo Equação de Bernoulli
Relembrando da equação de Bernoulli aplicada para processos com máquinas de fluxo...
Onde,
-H é a altura de carga da bomba, que é a energia que a bomba deve fornecer ao sistema;
-Δp é a variação de pressão do sistema;
-ΔV2 é a variação de energia cinética do sistema;
-Δz é a variação de energia potencial do sistema;
-hLT é a perda de carga total do sistema, devido ao atrito do fluido com a tubulação e ao atrito com os acessórios;
-ρ é a densidade do fluido;
-g é a constante da gravidade, g=9,81 m/s2.
Para hLT
Onde,
-hp e hac são a perda de carga devido ao atrito do fluido com a tubulação e a perda de carga devido ao atrito com os acessórios, respectivamente;
Passo 3
Aplicando o balanço de energia mecânica (Eq de Bernoulli) entre o reservatório de baixo no nível do mar (1) e o reservatório de cima (2), da figura PA11.4, lá em cima no enunciado
Onde,
-p1 e p2 são a pressão no reservatório de baixo e no de cima, respectivamente;
-V1 e V2 são a velocidade do fluido no reservatório de baixo e no de cima, respectivamente;
-z1 e z2 são a altura no nível no reservatório de baixo (nível do mar) e no nível de cima (topo do reservatório), respectivamente;
-hLT é a perda de carga total;
-ρ é a densidade da água, ρ=998 kg/m3;
-g é a constante da gravidade, g=9,81 m/s2.
Na Eq1 não foi adicionado o termo hac, pois foi pedido para desprezar as perdas localizadas, isto é, as perdas com acessórios.
Isolando H
Passo 4
Vamos agora analisar a figura PA11.4, lá em cima para ver quem é quem da equação de Bernoulli.
Analisando o esquema da figura PA11.4, vemos que
Onde, patm é a pressão atmosférica que você pode considerar para as duas pressões, pois os dois reservatórios estão abertos para a atmosfera.
Também vemos que as velocidades em 1 e 2 são referentes as velocidades de nível de fluido nos reservatórios, e como estes são de grande dimensão (D muito alto), então as velocidades são muito pequenas. Assim,
Já para as alturas z1 e z2, temos pela figura que
A Eq. da altura de carga da bomba, H agora é
Passo 5
Pela equação de Darcy-Weisbach
Onde,
-hp é a perda de carga principal por atrito na tubulação;
-f é o fator de atrito;
-LT é o comprimento total da tubulação;
-DT é o diâmetro interno da tubulação;
-V é a velocidade do fluido na tubulação;
-g é a constante da gravidade, g=9,81 m/2.
Para a perda de carga localizada, hac
Onde,
-hac é a perda de carga localizada;
-Ki é uma constante que é especifica para cada tipo de acessório na tubulação;
Passo 6
Substituindo as expressões de perda de carga na Eq2
Para expressarmos em termos de vazão, podemos usar a seguinte relação entre vazão e velocidade de escoamento
Onde,
-Q é a vazão volumétrica;
-A é a área da seção transversal do tubo;
-V é a velocidade do fluido.
A área de seção transversal é função do diâmetro da tubulação
Assim,
Isolando V
Substituindo na Eq3
Onde,
Passo 7
Vamos agora determinar o fator de atrito f.
O fator de atrito depende de Re e da rugosidade relativa...
Pelo problema 6.62, o tubo é de ferro fundido e para este material a rugosidade, ε, vale
...Equação de Reynolds
Onde,
-Re é o número de Reynolds;
-ρ é a densidade do fluido (água), ρ=998 kg/m3 para a água;
-DT é o diâmetro da tubulação, DT=38 cm=0,38m;
-Q é a vazão do fluido;
-μ é a viscosidade dinâmica do fluido (água), μ=0,001 kg/m.s para a água;
Veja que Re depende da vazão, Q, e não temos esse valor. Você tem duas alternativas para isso. Você pode fazer um cálculo iterativo, ou de forma mais simples você pode estipular um valor de Q, pegando dentro da faixa de valores de Q das figuras 11.7 que representam as bombas.
Você pode fazer isso, justamente porque foram fornecidos os dados de operação das bombas, e poderá corrigir o valor da vazão depois para o valor correspondente ao máximo rendimento.
Assim, pela figura 11.7a (ou 11.7b, tanto faz), pegando o valor na faixa do maior rendimento (88%)
Assim,
Pelo diagrama de Moody
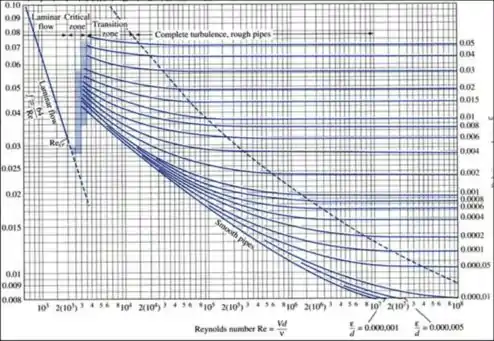
Passo 8
Calculando a altura de carga H pela Eq4
Aplicando os valores
Passo 9
(A)
Vamos agora usar esse valor de H=80 m encontrado para determinar qual é a bomba mais apropriada para o processo.
Fazendo uma análise nas figuras vemos que para o valor de H=80m para a bomba da figura 11.7a, o máximo rendimento que ela atinge para esse valor de H é uns 82% e para a bomba da figura 11.7b, ela atinge uns 88%. Portanto a bomba que atinge o maior rendimento máximo é a bomba da figura 11.7b
Passo 10
(B)
Voltando na figura 11.7b, já que essa é da bomba apropriada, vamos pegar o valor correspondente para a vazão. Pela figura
Passo 11
(C)
Também pela figura 11.7b
Passo 12
(D)
Para sabermos se a bomba está livre da cavitação, temos que calcular o parâmetro NPSH para o sistema, usando a eq. 11.20 do White, e comparar com o NPSH da bomba da figura 11.7b.
A condição de não cavitação é:
Se a condição acima for atendida, então a bomba não cavitará.
Pela eq. 11.20 do White
Onde,
-NPSH é a altura positiva líquida de sucção (Net Positive Suction Head), que é usado para avaliar a cavitação;
-pa e pv são a pressão absoluta da água no ponto de captação (reservatório no nível do mar, ponto 1) e a pressão de vapor da água, respectivamente;
-ΔzSucção é a diferença de altura do nível do reservatório no nível do mar (ponto 1) até a entrada da bomba. Pela figura PA11.4, ΔzSucção=-1,0m;
-hLT,Sucção é a perda de carga total na seção da tubulação da sucção da bomba;
-ρ é a densidade da água, ρ=998 kg/m3;
-g é a constante da gravidade, g=9,81 m/s2.
Passo 13
Determinando as pressões
A pressão do reservatório é a pressão atmosférica, pois o reservatório está aberto
A pressão de vapor (pv) podemos determinar usando uma tabela de dados para a água saturada. Pela Tabela 11.A6 do White, na T=20ºC
Determinando hLT,Sucção
Pela equação de Darcy-Weisbach
Assim,
Em termos de Q
Antes da entrada da bomba
Onde,
-Kentrada é perda de carga localizada em uma entrada, no caso entrada da bomba, Kentrada=1;
Aplicando os valores
A diferença de altura entre o nível do reservatório e a entrada bomba é 1,0 m, mas como o reservatório está abaixo do nível da bomba, então você deve atribuir um sinal negativo.
Passo 14
Calculando NPSHsistema
Comparando com o NPSHBomba obtido pela figura 11.7b
Em comparação
Logo, ocorrerá cavitação da bomba.
Resposta
A)
Bomba da figura 11.b, com rendimento máximo de 88%.
B)
C)
D)
Haverá cavitação!