Uma pequena bola de aço de raio , colocada no topo de uma esfera muito maior, de raio , começa a rolar sob a influência da gravidade. As resistências de rolamento e do ar são desprezíveis. Quando a velocidade da bola aumenta, ela deixa a superfície da esfera e torna-se um projétil. Determine o local em que a bola perde o contato com a esfera.
Passo 1
Vamos lá, pessoal! Nesse problema a questão nos deu uma esfera de raio colocada no topo de outra esfera maior, com raio :
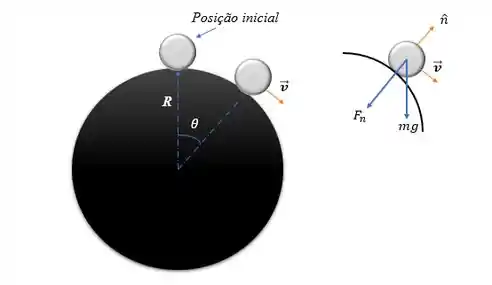
Para encontrar o local em que a bola perde o contato com a esfera precisamos fazer o somatório de forças na direção normal, . Assim,
Onde é a aceleração centrípeta, dada por:
O contato é perdido quando a força . Então,
Passo 2
Como as resistências de rolamento e do ar são desprezíveis, a energia é conservada ( e nós temos:
Isolando o :
Passo 3
Agora vamos combinar as equações dos passos 1 e 2 para obter o valor de .
Então,