Para uma pequena partícula de isopor (1 lbm/ft³) (esférica, com diâmetro d = 0,3 mm), caindo em ar padrão a uma velocidade V, a força de arrasto é dada por onde é a viscosidade do ar. Partindo do repouso, determine a velocidade máxima e o tempo que a partícula leva para atingir 95% dessa velocidade. Trace um gráfico da velocidade em função do tempo
Passo 1
Fala pessoal!! Tudo certo? Aqui temos mais um problema bem interessante de mecânica dos fluidos. Bora lá!?
Primeiramente, vamos separar todos os dados disponíveis:
Passo 2
Vamos lá, para esse exercício usaremos a equação da densidade da esfera, logo, sabemos que:
Sendo assim, sabemos também que a massa da esfera é densidade sobre o volume, logo:
Agora vamos calcular a massa da esfera:
Passo 3
Agora, pela 2ª Lei de Newton, vamos utilizar o estado em repouso, para isso, temos:
Encontraremos a velocidade máxima ignorando os efeitos da flutuação:
Passo 4
Voltando para a 2ª Lei de Newton em um estado geral, obtemos:
Passo 5
Esse exercício ele cairá em uma EDO para que possamos resolver (embora não seja o nosso foco), mas, vamos lá:
Substituindo os dados e a velocidade por 95% da máxima, encontramos:
Passo 6
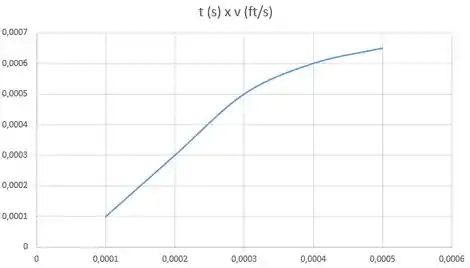
Por fim, vamos plotar o gráfico:
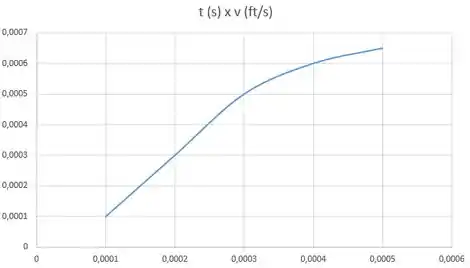
Essa resolução te ajudou? Responde Aí! Até a próxima, tchaaaau!
Resposta