O perfil de velocidades no volume de controle anular do Exemplo 3 é aproximadamente linear, variando de uma velocidade zero na fronteira externa para um valor de ωd/2 na fronteira interna. Desenvolva uma expressão para a velocidade do fluido, υ(r), em que r é a distância a partir do centro do eixo.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Desenhando a fronteira do eixo rotativo
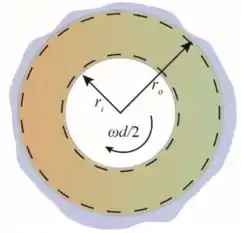
Passo 2
Como o perfil de velocidade no volume de controle anelar é linear, então consideramos uma relação linear entre a velocidade e o raio do eixo
Aqui, e são constantes e é a distância do centro do eixo.
Aplicando a condição de fronteira da superfície externa onde o raio é
Substituindo e na equação
Passo 3
Aplicando a condição de fronteira da superfície interna onde o raio interna é
Substituindo e na equação
Passo 4
Substituindo o resultado encontrado para na equação encontrada para
Substituindo os resultados que a gente obteve para e na equação para