Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 55
Um procedimento usual para o resfriamento de um circuito integrado (chip) para computador de alto desempenho envolve a fixação do chip a um sumidouro de calor no interior do qual são usinados microcanais circulares. Durante a operação, o chip produz um fluxo térmico uniforme q’’c na sua interface com o sumidouro de calor, enquanto um refrigerante líquido (água) é passado pelos canais. Considere um chip quadrado e um sumidouro de calor, ambos com L × L de lados, e com microcanais com diâmetro D e passo S = C1D, sendo a constante C1 maior do que a unidade. Água é fornecida a uma temperatura de entrada de Tm,ent e a uma vazão mássica total m (para todo o sumidouro de calor).
(a) Admitindo q’’c que se disperse ao longo do sumidouro de calor de tal modo que um fluxo q’’s térmico uniforme seja mantido na superfície de cada canal, obtenha expressões para as distribuições longitudinais das temperaturas média do fluido, Tm(x), e superficial, Ts(x), em cada canal. Em cada canal, considere escoamento laminar plenamente desenvolvido ao longo de toda a extensão e expresse os seus resultados em termos de m, q’’c , C1, D, e/ou L, assim como das propriedades termofísicas apropriadas.
(b) Para L = 12 mm, D = 1 mm, C1 = 2, q’’c = 20 W/cm2, m = 0,010 kg/s e Tm,ent = 290 K, calcule e represente graficamente as distribuições de temperaturas Tm(x) e Ts(x).
(c) Um objetivo comum ao se projetar esses sumidouros de calor é o de maximizar q’’c mantendo o sumidouro a uma temperatura aceitável. Sujeito aos valores especificados de L = 12 mm e Tm,ent = 290 K, e à limitação de que Ts,máx ≤ 50°C, explore o efeito de variações no projeto do sumidouro e nas condições operacionais sobre q’’c .
Passo 1
Vamo analisar o enunciado junto pra entender o que ele quer de você.
Temos um chip com microcanais circulares de diâmetro , por onde escoa água a uma vazão , com um fluxo térmico uniforme sendo mantido na parte externa do chip, fazendo com que um fluxo térmico uniforme seja mantido na superfície dos microcanais, como mostra o esquema ilustrativo abaixo:
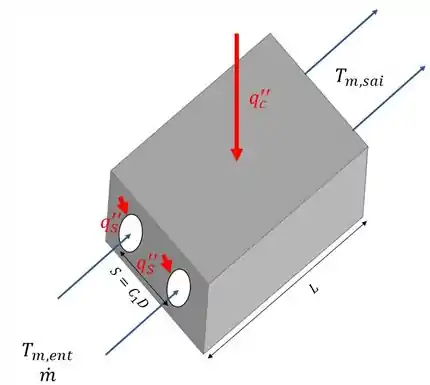
Onde é a distância entre um microcanal e outro.
Pra resolver essa questão, em primeiro lugar, a gente vai encontrar expressões para as distribuições das temperaturas média do fluido ((x)) e superficial ((x)), em cada canal, deixando em termos de , , , e , e as propriedades termofísicas da água.
Depois, vamos utilizar as expressões que deduzimos para representar graficamente (x) e (x) ao longo do espaço.
Por fim, vamos utilizar essas mesmas expressões deduzidas para mexer em algumas condições e analisar a variação de .
Para isso, vou te mostrar algumas equações que a gente vai usar.
Em primeiro lugar, o calor trocado ao longo dos tubos pode ser expresso a partir da seguinte equação:
Mas como temos um fluxo térmico constante na superfície do tubo, a taxa convectiva pode ser expressa como:
E esse fluxo superficial pode ser calculado como:
Por fim, temos que a expressão que pode ser calculada a partir dessa expressão:
E, portanto, podemos encontrar uma expressão para utilizando as duas últimas equações acima:
Pra resolver a questão, vamo precisar buscar as propriedades da água líquida saturada na Tabela A.6 (página 640) a uma temperatura de :
Caramba, foi muito informação né? Agora a gente vai resolver a questão nos próximos passos.
Passo 2
Primeiro, vamo resolver o item (a).
Devemos pegar as equações que deduzimos no Passo 1 para (x) e (x) e expressá-los em termos de , , , e .
Em primeiro lugar, devemos lembrar que temos microcanais no chip, que devemos calcular com base na largura do chip e na distância entre cada microcanal . Portanto:
Depois, devemos colocar o fluxo térmico na superfície do tubo em função do fluxo térmico na superfície do chip . Vamos partir do pressuposto que a taxa de calor se conserva, então teremos a seguinte igualdade:
O que significa dizer que a soma de todas as taxas de calor na superfícies dos microcanais é igual à taxa de calor na superfície inteira do chip.
Mas como demonstramos que , a expressão para vai ser:
Portanto, as expressões para (x) e (x) vão ficar assim:
Passo 3
Agora, vamo resolver a letra (b).
Vamos pegar os valores das propriedades da água que a gente buscou no Passo 1 e os valores de , , , e e fornecidos no enunciado da letra (b), e substituir nas expressões para (x) e (x) que deduzimos no Passo 2.
Além disso, vamos lembrar que para um fluxo laminar num escoamento interno com fluxo constante na parede do tubo, o número de Nusselt é . Portanto, o coeficiente de convecção pode ser calculado como .
Substituindo tudo isso nas expressões para (x) e (x):
Agora sim, podemos usar essas expressões para traçar gráficos no Excel de a e determinar a distribuição de temperatura da temperatura média no tubo e a temperatura da superfície:
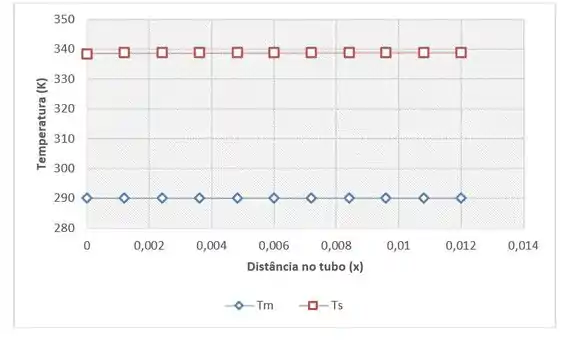
Passo 4
Agora, pra finalizar a questão, a gente vai combinar as expressões para (x) e (x) que deduzimos no Passo 2 e vamos brincar um pouco com algumas variáveis neles para poder testar a variação de com :
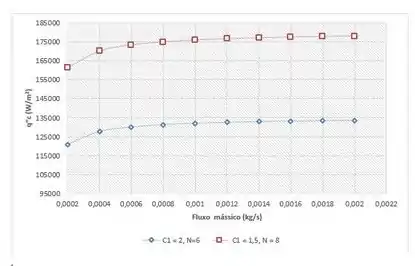
Agora vamos analisar o que queremos fazer nesse item (c). Basicamente, a gente quer encontrar formas de maximizar quando temos . Para as condições que a gente tem, um regime turbulento seria alcançado com Pra analisar essa variação mantendo o coeficiente de convecção que a gente calculou, vamos variar o fluxo mássico de a , para dois valores de , : 2 e 1,5.
Sendo assim, vamos traçar o gráfico no Excel para esse caso:
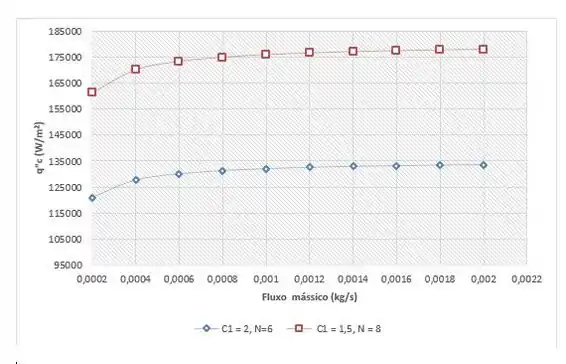
Vamo analisar esse gráfico agora.
Quando aumentamos o valor de , diminuímos o número de tubos e, por consequência, os valores de são bem menores. Além disso, podemos perceber que para maiores valores de vazão mássica, também obteremos maiores valores de .
Portanto, para maximizar , devemos utilizar baixos valores de e altos valores de
UFA, demorou, mas a gente acabou de matar a questão juntos!
Resposta
(a) As expressões para a temperatura média e a temperatura da superfície são: e
(b)
(c)
