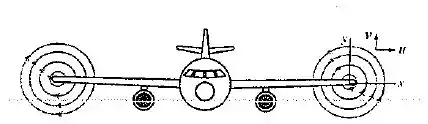
Nós sempre observamos a formação de escoamentos circulares (vórtices) nas pontas das asas dos aviões quando estes estão voando sob certas condições, os escoamentos circulares podem ser aproximados pelos campos de velocidade e , onde K é uma constante definida pelas características do avião considerado. Observe que tanto x como y são medidos a partir do centro dos escoamentos circulares. (a) Mostre que a velocidade nesses escoamentos é inversamente proporcional a distância da origem, . (b) Prove que as linhas de correntes desses escoamentos são circulares.
Passo 1
Falaaa pessoal, como vocês estão? Bom, bora pra mais uma questão desse assunto!
- Lá do problema anterior e dessa situação em geral, a gente tem as seguintes igualdades pras componentes da aceleração:
- Semelhante ao item anterior temos:
Da ilustração a seguir, notamos que .
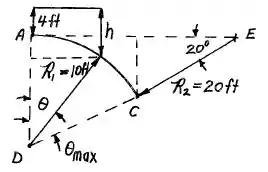
Logo, vamos ter:
Ou seja:
Essa igualdade é válida desde que o ângulo esteja entre o zero e seu ângulo máximo, sendo que seu ângulo máximo é igual a .
Passo 2
Da figura abaixo, a gente vai ter as seguintes relações:
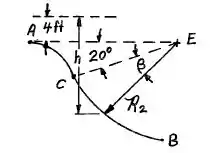
Logo, teremos que:
Ou seja, e finalmente:
Com
Essa igualdade vai estar valida desde que o ângulo fique no intervalo entre 0 e 70°.
Resposta
- Com
Essa igualdade é válida desde que o ângulo esteja entre o zero e seu ângulo máximo, sendo que seu ângulo máximo é igual a .
Essa igualdade vai estar valida desde que o ângulo fique no intervalo entre 0 e 70°.