Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 5.Problemas - Ex. 10
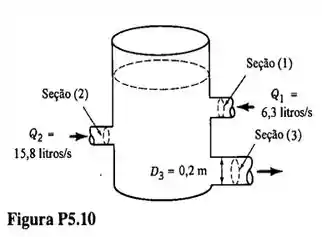
O tanque cilíndrico mostrado na Fig é alimentado pelas seções (1) e (2) com as vazões indicadas na Figura. Determine a velocidade média na seção de descarga do tanque, sabendo que o nível da água no tanque permanece constante ao longo do tempo.
Passo 1
Bom! Mais uma aí, galera!
Vimos na teoria que em escoamento incompressível e permanente o que entra tem que ser igual ao que sai, pois o volume do nosso sistema é fixo e nosso fluido é incompressível.
Assim tudo que entra é igual a tudo que sai:
A gente sabe que o fluido entra em com uma vazão de também em com uma vazão de e sai em com uma vazão que não é dada...
A gente precisa então, montar uma equação com entradas e saídas, certo?
Vamos montar a equação de entradas e saídas:
Passo 2
Pronto! Essa é a equação que vai ajudar a gente a resolver nosso problema!
Isolando que é o que a gente quer...
E substituindo os valores numéricos, encontramos nossa resposta: