Um tipo comum de viscosímetro para líquidos consiste em um reservatório relativamente grande, com um tubo de saída muito delgado. A vazão de saída é determinada pelo tempo de queda do nível da superfície. Se óleo de densidade constante sai do viscosímetro mostrado a uma vazão de 0,273 cm3/s, qual é a viscosidade cinemática do fluido? O diâmetro do tubo é 0,18 cm.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
A figura aqui embaixo mostra o reservatório que o óleo está fluindo pelo tubo
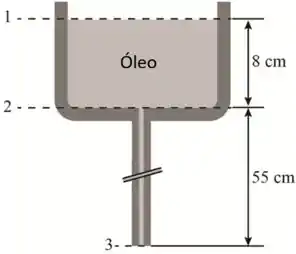
No reservatório o nível de óleo é denotado por 1, a base do reservatório é de onde o escoamento passa para o tubo e é denotado por 2 e a saída é denotada por 3.
Calculando a descarga de velocidade :
Área do tubo é dada por:
A descarga de velocidade é dada por:
Aqui, a taxa de escoamento do óleo do viscosímetro é
Passo 2
Aplicando a equação de Bernoulli de 1 à 2:
Aqui, temos:
1. pressão na seção 1 é a pressão atmosférica,
2. pressão na seção 2,
3. velocidade do escoamento na seção 1,
4. velocidade do escoamento na seção 2,
5. diferença no nível entre a seção 1 e 2,
6. densidade do óleo,
7. aceleração da gravidade,
Assumindo que a velocidade do óleo permanece constante enquanto ele viaja pelo tubo.
Substituindo , já que o fluido começa do repouso, e
Passo 3
O escoamento através do tubo, então terá uma perda para atrito.
A perda por atrito é dada por:
De acordo com a equação de Hagen-Poiseuille, o gradiente de pressão é dado por:
Para as condições dadas, podemos reescrever:
Aqui, temos:
1. viscosidade do óleo,
2. velocidade do fluido,
3. diâmetro do tubo,
4. comprimento do tubo,
5, diferença na pressão entre os dois finais do tubo,
Passo 4
Substituindo o valor de para obter uma expressão para a perda pelo atrito:
Passo 5
Aplicando a equação de Bernoulli de 2 à 3:
Aqui, temos:
1. pressão na seção 2,
2. pressão na seção 3 é a pressão atmosférica,
3. velocidade do escoamento na seção 2,
4. velocidade do escoamento na seção 3,
5. diferença no nível entre a seção 2 e 3,
6. densidade do óleo,
7. aceleração da gravidade,
8. perda para atrito,
Já que a velocidade do óleo permanece constante pelo escoamento do tubo, então
Passo 6
Igualando os valores obtidos no Passo 5 e Passo 2, temos:
Substituindo o valore de
Passo 7
Obtendo valores de :
O comprimento do tubo é:
O diâmetro do tubo é:
Passo 8
Substituindo os valores para determinar a viscosidade cinemática do óleo: