Uma torre de resfriamento refrigera água quente, pulverizando-a contra um escoamento forçado de ar seco. Uma parte da água evapora nesse ar e é carregada para atmosfera fora da torre de resfriamento; a evaporação resfria as gotas de água remanescente, que são colocadas no tubo de saída da torre (com 6 in de diâmetro interno). Medições indicam que a vazão de água quente é de 250.000 lb/h e que a água fria (70 °F) escoa a uma velocidade média de 5,55 ft/s no tubo de saída. A vazão do ar úmido deve ser obtida a partir de medições da velocidade em quatro pontos, cada um representando ¼ da área da seção transversal da corrente de ar igual a 13,2 ft2. A massa específica do ar úmido é 0,066 lb/ft3. Determine (a) as vazões mássica e volumétrica da água fria, (b) a vazão mássica do ar úmido e (c) a vazão mássica do ar seco.
Passo 1
Vamos lá! O nosso volume de controle é a torre de resfriamento. A questão nos deu os dados sobre o fluxo de entrada e saída nela.
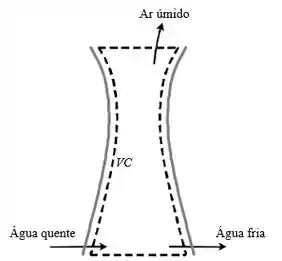
Precisamos encontrar (a) as vazões mássica e volumétrica da água fria, (b) a vazão mássica do ar úmido e (c) a vazão mássica do ar seco. Para isso, vamos usar a equação da continuidade:
E em cada entrada e saída:
Beleza, então temos na saída de água fria:
Sabendo que , e que segundo o enunciado e , temos:
Então,
𝑓𝑟𝑖𝑎=1,09 𝑓𝑡3𝑓𝑟𝑖𝑎=1,09 𝑓𝑡3
O fluxo mássico é dado por:
Assim, tendo a densidade da água , temos:
Ou
Encontramos as vazões mássica e volumétricas da água para esse caso, agora vamos encontrar as vazões mássicas do ar úmido e do ar seco.
Passo 2
Para o fluxo de ar, vamos usar a equação da continuidade para balancear o fluxo de água:
Assim,
Este é o fluxo mássico de vapor de água. Nós vamos usar isso para obter o fluxo de ar através da equação:
Onde é a umidade relativa e a questão nos deu a densidade do ar úmido
Então,
Para a densidade do ar seco, podemos utilizar a densidade do ar atmosférico, que é tabelada:
Convertendo,
Assim,
Onde e também são tabelados. E temos:
Passo 3
Com esses dados podemos agora substituir na equação:
E a vazão mássica do ar úmido é
Resposta
(a) e
(b)
(c)