Um tubo de Stefan de 2,5 cm de diâmetro é utilizado para medir o coeficiente de difusão binário de vapor de água no ar a 25°C e 95 kPa. O tubo é parcialmente cheio de água com uma distância da superfície da água à extremidade aberta do tubo de 25 cm. Ar seco é soprado sobre a extremidade aberta do tubo, de modo que o vapor de água que sobe ao topo é removido imediatamente e a concentração de vapor no topo do tubo é zero. Durante 10 dias de operação contínua, a uma pressão e uma temperatura constantes, a quantidade de água evaporada é 0,0011 kg. Determine o coeficiente de difusão do vapor de água no ar a 25°C e 95 kPa.
Passo 1
Vamos reunir nossas informações. Temos água evaporando em um tubo de Stefan nas condições de e .
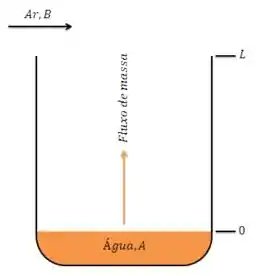
O processo de transferência de massa ocorre dos pontos z=0 até z=. Sabemos que no topo (z=) não há água. Então .
Vamos considerar que na interface líquido-gás (z=0), o ar está saturado de água. Então . Sabemos que o tubo tem diâmetro e que após 10 dias, nessas mesmas condições, foram evaporados 0,0011 kg de água. O exercício nos pede para determinar o coeficiente de difusividade do vapor de água no ar. Vamos lá?
Passo 2
Nosso primeiro passo será determinar o fluxo molar de água. O fluxo molar pode ser descrito como:
Não temos a quantidade de mols de água que evaporaram, porém já temos a área exposta do tubo e o tempo. Também já temos a massa evaporada. Então vamos transformar esta massa em número de mols a partir de:
A massa molar da água é . Então:
Substituindo este valor na fórmula de fluxo:
Passo 3
Antes de continuar vamos fazer algumas considerações. Vamos considerar que o ar não difunde para o interior da fase líquida da água (difusão de A em B estagnado). A concentração molar na fase gasosa é e é constante. Agora que estamos de acordo vamos prosseguir. O fluxo molar para a situação de A em B estagnado pode ser calculada por:
Temos quase todas as variáveis, restando determinar apenas e . A fração molar pode ser calculada por:
Voltando para a equação de fluxo:
Resposta
A difusividade do vapor de água no ar é de .