Uma tubulação de 40 km de comprimento transporta petróleo a uma vazão de 4000 barris por dia. A queda de pressão resultante é 3,45 × 106 Pa. Se uma tubulação paralela de mesmo tamanho for colocada ao longo dos últimos 18 km da primeira tubulação, qual será a nova capacidade dessa rede? O escoamento em ambos os casos é laminar e a queda de pressão permanece 3,45 × 106 Pa.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Escrevendo a equação Hagen-Poiseuille
Aqui, temos:
1. viscosidade do fluido,
2. velocidade média do escoamento,
3. diâmetro do tubo,
4. gradiente de pressão,
E o sinal negativo representa que a pressão cai ao longo do escoamento
Para essas condições, a equação se torna
Aqui, temos:
1. diminuição na pressão,
2. comprimento do único tubo,
Passo 2
Escrevendo a relação para a velocidade média do escoamento no tubo
Aqui, temos:
1. quantidade de petróleo entregada por dia,
2. área da seção transversal do tubo,
Substituindo
Passo 3
Desenhando o tubo simples que o fluido passa (Caso 1)
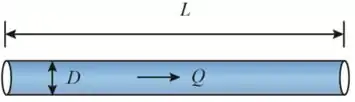
Considerando o Caso 1, substituindo para
Passo 4
Desenhando o tubo simples e paralelo que o fluido passa (Caso 2)
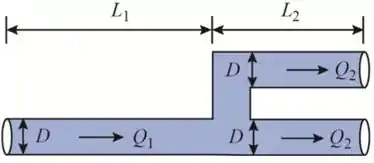
Considerando o caso 2, uma linha paralela de mesmo diâmetro está ao longo dos últimos
Para uma combinação de tubo simples e paralelo:
1. comprimento da última porção do tubo,
2. comprimento da primeira porção do tubo,
Escrevendo a expressão para a queda de pressão ao longo da primeira porção do tubo simples e paralelo
Aqui, a descarga através da primeira porção é
Substituindo
Passo 5
Escrevendo a expressão para a queda de pressão ao longo do tubo paralelo
Substituindo
Aqui, a descarga através do tubo paralelo é
A descarga através da primeira porção do tubo é igual a soma de descargas dos dois tubos paralelos
Passo 6
A queda de pressão em ambos os casos 1 e 2 permanece constante
A queda de pressão relaciona entre ambos os casos
Substituindo os valores de , e
Passo 7
Substituindo
Substituindo para obter a capacidade